Difference between revisions of "Space Based Solar Power"
Exoplatz.org>Hkhenson |
(Reworking start of article a little.) |
||
| (118 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | '''Space Based Solar Power''' is the concept of moving the collection of energy from [[Sol]] to Earth orbit in order to increase collection efficiency, eliminate weather, time-of-day, and seasonal outages, and reduce needed land usage. Energy collectable from orbit is a major factor in the first level of the [[Kardashev Scale]]. | |
| − | = | + | ==What are Power Satellites?== |
| + | <!-- The history is covered in the Wikipedia article above. The 1968 work by Peter Glaser is briefly mentioned in the video here: https://www.youtube.com/watch?v=VEkZkINrJaA | ||
| + | --> | ||
| + | They are a way to collect solar power out in space, usually GEO where the sun shines 99% of the time. Solar power on the ground has the problems of intermittency from clouds, night and the sun being low in the sky. Typically, ground solar in good locations averages about 20% of its peak rating. Power satellites are subject to short eclipses (up to 70 minutes) near the equinoxes around midnight. Because demand is low, the interruptions can be tolerated. With deep market penetration, the microwave beams can be crossed if the demand exceeds the capacity of the surface grid to redistribute power east to west or west to east. | ||
| − | + | They potentially scale to more than ten times the current energy needs of the human race. Started soon and pushed hard, they could end the build up of CO2 in the atmosphere and even reverse it. | |
| − | + | If power satellites reach a high market penetration at times the power demand will go below their output. Power in excess of current demand can be fed to synthetic fuel plants solving the liquid transport fuel problem as well. | |
| − | == | + | ===Methodology of This Work=== |
| + | The specifics in this study are less important than the analysis methodology. Important concepts include levelized cost of power, specific mass in terms of kg/kW, lift cost, ERoEI, and payback times. The attempt here will be to analyze specific examples but the details of choices such as PV vs thermal are less important than the analysis procedure. | ||
| − | |||
| − | + | ==Power Satellites and Energy Economics== | |
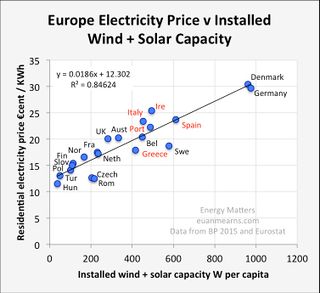
| + | In the absence of other forces (such as legal requirements to buy renewable energy) power satellites compete in the energy market. Of all energy forms, electrical energy is the ultimate standard commodity. When a customer plugs in a toaster, there is no way to tell what source the energy came from. At the end of the month, they pay the bill at the rate set by the power company under the oversight of a utility commission. One level up, the power companies are hemmed in by regulations that they buy (or make) the lowest cost electricity, with exceptions in some places that they have to purchase certain amounts of renewable energy. Wind and (ground) solar are both intermittent, requiring other sources or expensive storage to provide reliable power. The capital cost of intermittently run backup power either bankrupts the utilities or results in very high electrical rates. This is the current situation: the higher the fraction of renewable, the higher the consumer cost of electricity. | ||
| − | + | [[File:Mearns.jpg|320px]] | |
| − | + | The reason for the higher cost for systems that includes a lot of renewable power is not hard to understand. Wind and solar are intermittent. If steady, reliable power is desired then alternate sources of power are required. The capital cost of these backup sources must be included in the systemwide average cost of power in addition to the capital and maintenance cost of the wind or solar. | |
| − | + | Space based solar power is renewable but not intermittent. That should make it easier to sell power from space at a premium. However, governmental energy policy changes unpredictably over time. An alternative would be a "design to cost" effort where the target cost of power is low enough to get a large market share without government intervention. Competing on cost is the way discount suppliers of many commodities obtained a substantial market share. (Examples, Southwest Airlines, GEICO, Charles Schwab.) | |
| − | + | ===Levelized Cost of Power=== | |
| − | + | The formula for the levelized cost to generate electricity is here: [https://en.wikipedia.org/wiki/Cost_of_electricity_by_source] | |
| − | + | This spreadsheet [https://docs.google.com/spreadsheets/d/1wDvn369EudkYGsPK3jNt4FmBFpNFtt0ZwDZl_lt_SNM/edit#gid=1481425448] assumes $1,600,000 per MW ($1600/kW) as the initial cost and 10% per year of the parts cost for maintenance. Power satellites supply base load. In the spreadsheet, it is assumed to be ~91% of the time. It may be higher. | |
| + | The discount rate used in the spreadsheet is 6.8%, same as the US government uses for other sources. The accounting period is 20 years, and no salvage value is assumed. | ||
| + | The ratio between the $1600/kW cost and the cost that comes out of the formula (~2 cents per kWh) is approximately 80,000 to one. Electric power cost is proportional to the cost of a power satellite (or any power source that has no fuel cost and low maintenance) in this ratio for this discount rate and years of service. | ||
| + | |||
| + | The UK government has determined that 3.5% discount is proper for projects of this kind. Using 3.5%, the electric cost comes out at just over 1.5 cents per kWh and ~100,000 to one. Extending the accounting period to 30 years at 3.5% brings the cost of power down to 1.24 cents per kWh and a cost of power to cost of investment ratio to ~130,000 to one. It is a live spreadsheet; try your own numbers. A ratio of 80,000 to one is conservative. | ||
| + | |||
| + | To take market share from coal will require the cost to be less than 4 cents per kWh for electricity from coal. Three cents per kWh allows a capital cost of $2400/kW. That, or less, is the "design to cost" target. | ||
| + | |||
| + | ===Cost Allocations=== | ||
| + | The current model has the $2400 target cost (from levelized cost above) split out as follows: | ||
| + | |||
| + | *$200/kW for the rectanna ($1 B for 5 GW), | ||
| + | |||
| + | *$900/kW for the cost of parts and minor labor in space and | ||
| + | |||
| + | *$1300/kW (6.5 kg/kW[[https://spacejournal.ohio.edu/issue18/thermalpower.html]] and $200/kg) for the cost of transport to GEO. (add pointer to sustech 2014 paper) | ||
| + | |||
| + | These numbers are targets which future work will firm up. If they go too high, something (like the cost charged for the electric power) will have to be adjusted. Of course, if they go too high, the entire idea needs to be reconsidered. | ||
| + | |||
| + | ===ERoEI (Energy Returned on Energy Invested) and Energy Payback Time=== | ||
| + | One of the metrics used to evaluate energy projects is energy | ||
| + | return on energy invested. This is expressed as a ratio, and for | ||
| + | shallow oil wells decades ago was typically 100 to one or higher. | ||
| + | i.e., number of barrels of oil needed to drill an oil well divided | ||
| + | into the number of barrels it produced. An alternate way more applicable to | ||
| + | renewable sources is the energy payback time. It's typically about | ||
| + | two years for PV or wind. | ||
| + | |||
| + | High ERoEI and short payback times usually accompany low cost. | ||
| + | |||
| + | Most of the energy embedded in a power satellite comes from the transport fuel. | ||
| + | |||
| + | ====Transport Energy==== | ||
| + | Combustion of hydrogen is 143 MJ/kg or 39.4 kWh/kg plus the energy needed to liquefy the hydrogen. Google for "A Future Energy Chain Based on Liquefied Hydrogen" (you may need to add Berstad) | ||
| + | and go down to page 20. There they cite a number of ~6.5 kWh/kg to liquefy hydorgen. A large industrial plant might | ||
| + | do a little better by warming the LNG before steam reforming with hydrogen to start the cooling. Ignoring that possible small improvement, the energy cost of LH2 is about 46 kWh/kg. | ||
| + | It's hard to say exactly where you should measure the input energy, | ||
| + | but the process to make hydrogen from natural gas is efficient, and (if we ship it as LNG) it | ||
| + | only uses about 1.7% of the energy in a kg of natural gas to liquefy it. I.e., | ||
| + | measuring at the well head will not make a great deal of difference. | ||
| + | The CO2 released by steam reforming of natural gas is about 2.5 times the hydrogen produced. | ||
| + | |||
| + | The current LEO to GEO hydrogen consumption (using electric | ||
| + | propulsion) is 4000 tons to get 15,000 tons to high orbit. On | ||
| + | average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 | ||
| + | tons of hydrogen reaction mass. I.e., 73% of the payload in LEO gets to GEO. At launch the average Skylon has 59 | ||
| + | plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload | ||
| + | 62 tons/11.84 tons or 5.25 kg/kg of payload. | ||
| + | |||
| + | The solar energy used to power the LEO to GEO transport is not | ||
| + | included since it is outside the Earth system. (The capital cost of the | ||
| + | propulsion power satellite is included in the financial models.) | ||
| + | |||
| + | For a power satellite specific mass of 6.5 kg/kW, a kW of power satellite (i.e., 6.5 kg) would use a little over 34 kg of LH2 to put it in GEO. | ||
| + | Using 46 kWh/kg for the energy content of LH2, that's around 1566 kWh of energy per kW of power satellite. | ||
| + | |||
| + | ====Parts Energy==== | ||
| + | Without a detailed list of the parts, materials and mass in a power | ||
| + | satellite, it's not easy to say how much energy goes into making the parts. | ||
| + | Aluminum has the most embedded energy at 15 kWh/kg. But not very much | ||
| + | will be aluminum. If we estimate 10 kWh/kg, the energy in the parts | ||
| + | would be ~650 kWh, for a total of 2216 kWh per kW of capacity. | ||
| + | |||
| + | When the power satellite is turned on, it takes 92 days (at 100% on | ||
| + | time) to repay the energy used to build it and move it to GEO. | ||
| + | |||
| + | That's a three-month energy repayment time. There are no other renewable | ||
| + | proposals that are even close. | ||
| + | |||
| + | If the power satellites last 30 years, you get an ERoEI of 120 to one, as good as early shallow oil wells. | ||
| + | |||
| + | This is subject to adjustment as we settle on more accurate numbers in | ||
| + | the design phase, but it is good enough to justify investigation in detail. | ||
| + | |||
| + | In his book on power satellites, John Mankins gives a payback time of 8 weeks. John uses the energy from physics, about 12 kWh/kg from the surface to GEO) (IIRC, it's actually 14.75 kW/kg)and doubles it twice for his estimate. | ||
| + | |||
| + | |||
| + | ==Power Satellite Types== | ||
| + | ===Photovoltaic (PV) and Concentrated PV=== | ||
| + | Most designs for power satellites since the 1970s have been PV. PV has advantages, long experience powering communication satellites being important. However, PV suffers from relatively low efficiency (20%) and degradation from radiation. There are proposals by Robert Forward and Robert Holt on draining the van Allen belt [http://en.wikipedia.org/wiki/HiVolt]; however, just the presence of a substantial number of power satellites in GEO is expected to greatly mitigate the radiation from particles trapped in the Earth's magnetic field. (The particles are stopped by running into a power satellite. There are only about 3 kg of protons trapped in the belts.) | ||
| + | |||
| + | There are PV cells that range up to 40% efficient, but they require concentrated light and cooling. The work on thermal power satellites makes CPV possibly attractive, though there are problems with the limited supply of gallium which is used to fabricated the multi-junction cells. | ||
| + | |||
| + | ===Thermal=== | ||
| + | Thermal (heat engines) power satellites are expected to eventually range up to 60% efficient, similar to combined cycle plants on earth. This means they need about 1/3 of the light interception area of ordinary PV, which reduces station keeping from light pressure. However, they also need radiator area that is about twice the sunlight interception area, (Bejan, 1997, pg 495, ref Bejan, A. Advanced Engineering Thermodynamics, 2nd ed. New York: Wiley, 1997.) Counting both sides of the radiator makes the exposed area for thermal and photovoltaic power satellites about the same. | ||
| + | |||
| + | ==Common Considerations== | ||
| + | ===Light Pressure and Mass=== | ||
| + | Light pressure is about 9 N/km^2 | ||
| + | |||
| + | The original studies done in the late 1970s came up with a mass of ~10 kg/kW. More recent realistic studies have averaged around 7 kg/kW. A few studies have proposed designs under one tenth of a kg/kW. Very light designs require a lot of station keeping against light pressure where designs in excess of 5 kg/kW can average the light pressure over a year. Because a substantial fraction of the construction cost is for transport to GEO, the mass of a power satellite is as important a number as the lift cost to GEO. This analysis will use 6.5 kg/kW. The number can be adjusted in the spreadsheets. | ||
| + | |||
| + | ===Energy Transmission Loss=== | ||
| + | How efficient is the transmission of the energy with the microwave beam? | ||
| + | |||
| + | For economic analysis, 50%. The loss chain might be a little better with technical improvements, but not much. It means you generate two kW in space for one kW on the rectenna bus. That's been assumed in all the analysis here. | ||
| + | |||
| + | ==Transport Methods Surface to LEO== | ||
| + | ===Falcon Heavy=== | ||
| + | Consider the projected Falcon Heavy, 53,000 kg to LEO, 121,400kg of | ||
| + | RP-1. That's about 2.3 kg of fuel for every kg lifted to LEO (here I assume that the entire mass in LEO is either reaction mass for the trip up or can be converted to power satellite parts--this may not be reasonable). RP-1 | ||
| + | is 42 MJ/kg, so the energy expended to LEO is about 96.2 MJ/kg or 26.7 | ||
| + | kWh/kg. You also have to lift the reaction mass for the LEO to GEO | ||
| + | leg so the fuel cost needs to be increased by around 20% giving 33.4 | ||
| + | kWh/kg. If the reaction mass is hydrogen, it's energy content is not | ||
| + | zero, hydrogen is close to 50 kWh/kg to make it and another 20 kWh/kg | ||
| + | to make it into a liquid. So to move a kg from LEO to GEO would take | ||
| + | 1/4 kg of LH2 at 70 kWh/kg or 17.5 kW/kg, for a total of ~51 kWh/kg. | ||
| + | At 10 kg/kWe (on the ground) 510 kWh will be required to move a kW of power sat to GEO. | ||
| + | At 100% on time, that's about 23 days to repay the energy. Unless I made an error, John's number is close enough. If only half of a Falcon Heavy payload becomes power satellite parts, John's estimate is very close. | ||
| + | |||
| + | ===Skylon=== | ||
| + | Much of the analysis been done using 50 kWh/kg as a ballpark number for hydrogen. It's good enough for rough calculations and it what it takes to make hydrogen if you are making it with electric power. | ||
| + | |||
| + | Combustion of hydrogen is 286 kJ/mol. Mole is 2.016 gm, so 496 moles in a kg, 143 MJ/kg or 39.4 kWh/kg. That's quite a bit less. The rough analysis have also been using 20 kWh/kg to liquify the hydrogen. That's way off. If you Google for "A Future Energy Chain Based on Liquefied Hydrogen" Berstad and go down to page 20, they cite a number of ~6.5 kWh/kg. We might do a little better because we can use warming the LNG to cool the hydrogen. That makes the energy content of the LH2 about 46 kWh/kg. It's hard to say exactly where you should measure the input energy, but the process to make hydrogen from natural gas is efficient, and it only uses about 1.7% of the energy in a kg of NG to liquify it. I.e., measuring at the well head will not make a great deal of difference. Still, this Wiki article needs to go into the thermodynamics of steam reforming. | ||
| + | |||
| + | ===Transport Methods LEO to GEO=== | ||
| + | The current LEO to GEO hydrogen consumption (using electric propulsion) is 4000 tons to get 15,000 tons to high orbit. On average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 tons of hydrogen reaction mass. At launch the average Skylon has 59 plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload 62/11.84 or 5.25 kg/kg of payload. | ||
| + | |||
| + | (Why hydrogen and not an inert gas? For a given amount of energy you can get considerably more exhaust velocity out of hydrogen.) | ||
| + | |||
| + | The solar energy used to power the LEO to GEO transport is not included since it is outside the system. (The capital cost of the propulsion power satellite is included in the financial models.) | ||
| + | |||
| + | Using my supported but perhaps optimistic number of 6.5 kg/kW, an installed kW would use a little over 34 kg of LH2 to get it in place. Using 46 kWh/kg for the LH2, that's around 1566 kWh per installed kW. | ||
| + | |||
| + | Without a detailed list of the parts materials and mass in a power satellite, it's not easy to say how much energy goes into the parts. Aluminum has the most embedded energy at 15 kWh/kg. But not very much will be aluminum. If we estimate 10 kWh/kg, the energy in the parts would be ~650 kWh, for a total of 2216 kWh per kW of capacity. | ||
| + | |||
| + | When the power satellite is turned on, it takes 92 days (at 100% on time) to repay the energy used to build it and move it to GEO. | ||
| + | |||
| + | That's a three month energy repayment time. I don't know of any other proposal that is even close. And the energy from a power satellite not intermittent. | ||
| + | |||
| + | If the power satellites last 30 years, you get an ERoEI of 120 to one. | ||
| + | |||
| + | This is subject to adjustment as we settle on more accurate numbers in the design phase, but it should be reasonably close. | ||
| + | |||
| + | ERoEI is an interesting metric, but the more important figure is the cost. Target cost is 3 cents a kWh falling to 2 cents within a few years. This just barely meets Gail's requirements. For a first approximation, the embedded energy in the parts and the energy required to make LOX are so small in comparison to RP1 or LH2 that they can be ignored. | ||
| + | |||
| + | It's surprising that even with a lower kg/kW number the energy payback time is longer for the Skylon. | ||
| + | |||
| + | ===Energy Payback Time, EROEI and Maximum Growth Rate=== | ||
| + | I recently ran an energy payback time for power satellites constructed using Falcon Heavy. It came in at around 8 weeks. | ||
| + | |||
| + | The current computation of LEO to GEO hydrogen consumption (using electric propulsion) is 4000 tons to get 15,000 tons to high orbit. On average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 tons of hydrogen reaction mass. At launch the average Skylon has 59 plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload 62/11.84 or 5.25 kg of hydrogen per kg of payload. | ||
| + | |||
| + | The solar energy used to power the LEO to GEO transport is not included since it is outside the system. (The capital cost of the propulsion power satellite is included in the financial models.) | ||
| + | |||
| + | Combustion of hydrogen is 286 kJ/mol. Mole is 2.016 gm, so 496 moles in a kg, 143 MJ/kg or 39.4 kWh/kg. If you Google for “A Future Energy Chain Based on Liquefied Hydrogen” Berstad and go down to page 20, they cite a number of ~6.5 kWh/kg. We might do a little better because we can use warming the LNG to partly cool the hydrogen. That makes the energy content of the LH2 about 46 kWh/kg. It’s hard to say exactly where you should measure the input energy, but the process to make hydrogen from natural gas is efficient, and it only uses about 1.7% of the energy in a kg of NG to liquify it. I.e., measuring at the well head will not make a great deal of difference. Still, we need to dig into the thermodynamics of steam reforming. | ||
| + | |||
| + | Using s perhaps optimistic number of 6.5 kg/kW, an installed kW would use a little over 34 kg of LH2 to get it in place. Using 46 kWh/kg for the LH2, that’s around 1566 kWh per installed kW. | ||
| + | |||
| + | Without a detailed list of the parts materials and mass in a power satellite, it’s not easy to say how exactly much energy goes into the parts. Aluminum has the most embedded energy at 15 kWh/kg. But not very much will be aluminum. If we estimate 10 kWh/kg, the energy in the parts would be ~650 kWh, for a total of 2216 kWh per kW of capacity. | ||
| + | |||
| + | When the power satellite is turned on, it takes 92 days (at 100% on time) to repay the energy used to build it and move it to GEO. | ||
| + | |||
| + | That’s a three month energy repayment time. We know of no other energy proposal that is even close. And the energy from a power satellite not intermittent. | ||
| + | |||
| + | If the power satellites last 30 years, you get an ERoEI of 120 to one. | ||
| + | |||
| + | This is subject to adjustment as we settle on more accurate numbers in the design phase, but it should be reasonably close. | ||
| + | |||
| + | ERoEI is an interesting metric, but the more important figure is the cost. Target cost is 3 cents a kWh falling to 2 cents within a few years. This just barely meets Gail’s requirements. | ||
| + | |||
| + | By the criteria given here https://en.wikipedia.org/wiki/Energy_cannibalism and here https://web.archive.org/web/20090817071517/http://www.climate2008.net/?a1=pap&cat=1&e=61 a power satellite growth rate of lower than 360% per year would result in lowering GHG emissions. | ||
| + | |||
| + | ===Reliability=== | ||
| + | Electric power needs to be reliable. First, the | ||
| + | power satellite size is only 5 GW. The target number is 3000 for 15 | ||
| + | TW. There would be spares sending power to low priority loads that | ||
| + | could be switched in less than a second to replace a higher priority failed one. Plus | ||
| + | we would still have the grid to distribute electricity from the | ||
| + | remaining powered rectennas, and for a long time, there would be other generation in the mix. | ||
| + | |||
| + | None the less, there are ways we could lose the whole fleet of them in | ||
| + | an instant if they were not designed to deal with it. In the year 774 or 775 | ||
| + | the Earth seems to have been hit with either a unprecedented solar flare or a fairly close gamma ray burst. | ||
| + | The latter are typically a few seconds, the former might take a few hours. In any case, it put a serious kink in the carbon | ||
| + | 14 for the next growing season. Such an event would take out the | ||
| + | controls for any power satellite that did not have enough shielding | ||
| + | around the control computers. The shielding needed against these 1000 | ||
| + | year events is considerably more than the worst solar flares observed to date. | ||
| + | |||
| + | Unlikely as they are, GRB or intense high energy solar flares are a concern that requires mitigation and recovery strategies | ||
| + | such as watch dog timers and hardened reboot memory. Radiation | ||
| + | resistance is an argument in favor of rotating machines rather than PV. | ||
| + | |||
| + | A solar flare can be seen coming and outside workers would probably have time to reach shelter. A GRB would be over before the workers had a chance to move. Neither are serious problems for people behind shielding good enough to stop cosmic rays. | ||
| + | |||
| + | ==Transport Earth to LEO== | ||
| + | ===SpaceX=== | ||
| + | [[SpaceX]] may not get the transport cost down low enough. It has to be to | ||
| + | be SSTO or possibly TSTO runway operations. | ||
| + | |||
| + | SpaceX _will_ eventually get the cost to GEO down by a full order of | ||
| + | magnitude, a remarkable achievement. Unfortunately this won't do it | ||
| + | for power from space, it takes _two_ orders of magnitude reduction. | ||
| + | Elon Musk knows this. It might be why he is so down on power satellites. | ||
| + | |||
| + | Note Oct 15,2016. | ||
| + | |||
| + | Musk was recently talking about a rocket with a cost of putting cargo into a Mars trajectory for $143/kg. That's remarkable and is low enough for power satellites to make economic sense. | ||
| + | |||
| + | ===Skylon=== | ||
| + | Until Reaction Engines demonstrated their high performance precooler, there were no realistic SSTO proposals out there. | ||
| + | |||
| + | [[www.reactionengines.co.uk/space_skylon.html]] | ||
| + | |||
| + | ====Skylon Doesn't Cause Much Ozone Damage (NOx)==== | ||
| + | NOAA worked out that up to a million Skylon flights per year there is little damage to the ozone. There is no point in solving the carbon and energy problem with power satellites if the cost is a billion cases of skin cancer. | ||
| + | |||
| + | The NOAA people put a lot of effort into modeling the problem, hundreds of hours of supercomputer time on the models, writing a paper and getting it through peer review. Highly appreciated. | ||
| + | |||
| + | The paper is available online at | ||
| + | |||
| + | http://onlinelibrary.wiley.com/doi/10.1002/2016EF000399/full | ||
| + | |||
| + | Click on the PDF symbol next to the journal title. | ||
| + | |||
| + | ==LEO to GEO== | ||
| + | |||
| + | ===Space Junk=== | ||
| + | Back in the late 70s, Boeing proposed building power satellite in LEO and then self powering to GEO (using ion engines or arcjets). They even did some nice artwork. But even in those days there was enough space to make this a very risky move and it was abandoned. HKH redid the math in recent years using the density of space junk given in the Wikipedia article. The result was that a power satellite would be hit almost 40 times while self powering to GEO. Almost all the hits are below 2000 km altitude. | ||
| + | |||
| + | Building power satellites in LEO would work, it's just they could not be moved to where they are useful unless the plan includes cleaning up the space junk first. | ||
| + | |||
| + | ===Engines=== | ||
| + | |||
| + | ====Arcjet==== | ||
| + | |||
| + | ====VSMIR==== | ||
| + | |||
| + | ===Power=== | ||
| + | |||
| + | ===Tug Rectenna=== | ||
| + | Increasing the frequency to 25 GHz and reducing the distance to half allows reducing the tug rectenna to 500 m. | ||
| + | |||
| + | This has not been optimized, nor have the tracking details worked out. | ||
| + | |||
| + | ===Worker Transport=== | ||
| + | Getting workers out to 12,000 km takes either a fast transport to keep the radiation exposure from the inner van Allen belt down or sending them up inside cargo containers. If they go up with power satellite parts around them for shielding, the trip is about 25 days. The return trip is shorter, around 5 days, but unless a lot of shielding is taken | ||
| + | |||
| + | ===Propulsion Power Satellite=== | ||
| + | |||
| + | ===Reaction Mass=== | ||
| + | |||
| + | ===Construction Orbit=== | ||
| + | |||
| + | ==Construction Site== | ||
| + | Tentatively we have selected 10,400 km, less than one third of the way to GEO. This is in a six hour orbit orbit. The choice is based on this altitude being the low radiation zone between the inner and outer van Allen belts. The orbit is subject to tradeoff/optimization studies which have not been done yet. | ||
| + | |||
| + | ===Platform (JIG)=== | ||
| + | Even more tentative, we have envisioned a kind of "dry dock" for power satellites. Big frame of beams to move cargo from the stacks to the work sites where the power satellites are constructed. We also project a rotating habitat with the spin axis pointing solar north/south and a concentrating reflector to bring light inside through a window. | ||
| + | |||
| + | ===Habitat--Company Town?=== | ||
| + | On the roughest of analogies dating back to Liberty ship construction in WW II, it might take 400 construction workers for the 10 per year pilot construction plant. This includes families. The shielding on the habitat will need to be ~six tons per square meter to reduce the cosmic radiation to the level seen on Earth. | ||
| + | |||
| + | The consequence for a 50 m habitat is 60,000 tons of shielding, about $9 B in lift cost at $150/kg. | ||
| + | |||
| + | It has to be a spinning habitat. One thing learned from the ISS is that neat as zero g is, human do not do well health wise in long term zero g. The spin rate for one g at the equator is 6 RPM. Do we spin the shielding or just the habitat? In either case, there is a considerable amount of rotational kinetic energy in the habitat. Whatever is used for a bearing must be proof against lockup. | ||
| + | |||
| + | There is a reason for families. We can't expect construction workers to live like monks or nuns. Taking them to and from 10,400 km (6 hour orbit) is either slow or very expensive in reaction mass and power. It is relatively easy to ship the workers and families up. They are shielded by containers of parts for the 25 days it takes to transit up. But there are no parts coming back down so shielding for returning workers would have to be carried at great cost. Alternately, they could go up in the habitat if it was constructed in LEO. | ||
| + | |||
| + | About the interaction of radiation, workers and transport . . . we might be able to build power satellites entirely using | ||
| + | robots directed from the ground or by AIs. We don't have such robots/AIs yet, but if the development time is short and the cost less than $9 B, that may be the way to go. (Teleoperated robots are closer and a 6 hour orbit does not induce as much speed of light delay as GEO.) I would be OK with that, though saddened by the loss of human | ||
| + | experience. Assuming we don't have robots building power satellites, | ||
| + | or at least they need help from people, then we have to have people in | ||
| + | space. For social and economy of scale reasons | ||
| + | fewer than about 200 may not make sense. If the ISS is any indicator, | ||
| + | one quarter of them will be working on maintenance to keep the habitat | ||
| + | liveable. | ||
| + | |||
| + | A power satellite project makes a lot of money but can it afford 200 | ||
| + | workers in space? Perhaps the least complicated analysis is to take | ||
| + | the income stream from 10-12 power satellites per year. That seems to | ||
| + | be the minimum were transport economies of scale kick in. 11 power | ||
| + | satellites at $11 billion each is $121 B. A thousand people would be | ||
| + | building $121 M per person, 500 would be building $242 M each. A pay | ||
| + | rate of a million per person per year would make the labor charges on | ||
| + | the product under half a percent. | ||
| + | |||
| + | We get the wages back at the company store where we charge them | ||
| + | $200/kg for steak. Just kidding! | ||
| + | |||
| + | After feeding the workers, the "used" food becomes part of a power | ||
| + | satellite so the effective cost to feed them is zero. If there is | ||
| + | nothing else to use it for, each power satellite needs a substantial | ||
| + | "space anchor." A "space anchor" is just a multi ton mass (anything | ||
| + | will do) on the end of a long string. It is connected to the | ||
| + | transmitter disk edges by a bridal and winches. It eliminates using | ||
| + | reaction mass for pointing the power satellite. (Gravity gradient | ||
| + | stabilization.) | ||
| + | |||
| + | So we can pay the workers and feed them. Next problem is getting them | ||
| + | out to the construction site. If we use 10,400 km (in the radiation | ||
| + | minimum between the van Allen belts) then the time for the reference | ||
| + | beamed energy transportation system is about 25 days up and about 5 | ||
| + | days back. In the Apollo program, | ||
| + | http://www.braeunig.us/apollo/VABraddose.htm, the astronauts skirted | ||
| + | around the belts and went fast so they didn't spend time in them. For | ||
| + | power satellites we have to bull right through the hottest part of the | ||
| + | Van Allen belt and slowly too due to the orbital mechanics of spiral | ||
| + | orbits. | ||
| + | |||
| + | However, we have something on the trip up the Apollo astronauts didn't | ||
| + | have, tens of thousands of tons of power satellite parts which can be | ||
| + | used for shielding. The scale of the cargo stacks is more or less set | ||
| + | by beamed energy microwave optics used to power the stack out to the | ||
| + | construction site. If made of Skylon sized containers, a cargo stack | ||
| + | has 11 layers of 91 containers per layer. If the modules for human | ||
| + | transport are buried a few layers down and in the center of the stack, | ||
| + | it's hard to imagine the relatively low radiation of the worst part of | ||
| + | the belt giving them much exposure (though it should be calculated). | ||
| + | |||
| + | An alternative would be to build the habitat in LEO and send it up with the workers inside. Depending on the propulsion power available, this could take a couple of months. | ||
| + | |||
| + | The exposure on the way down is 1/5th the time, but with no cargo to | ||
| + | shield them, the radiation exposure would be much larger, perhaps | ||
| + | lethal. | ||
| + | |||
| + | My solution to this problem is to send workers up one way. I.e., they | ||
| + | would be expected to stay at least ten years. That means that (unless | ||
| + | you plan on using monks) we have to send up families. That means | ||
| + | children, and that means controlling the radiation in the construction | ||
| + | habitat to no worse than the level at Denver and spinning the habitat | ||
| + | to one g. | ||
| + | |||
| + | ====Limited Recycling==== | ||
| + | Most food for the workers can be shipped up. It is essentially free since after people eat it, it can all be recycled into parts of a power satellite. Not so with fresh food that cannot survive a month shipping. Salad greens need to be grown in the habitat. This does not look like a hard problem and may eliminate some of the atmosphere contaminate problems that require burners in submarines. | ||
| + | |||
| + | ===Self Power (Out to GEO)=== | ||
| + | In terms of reaction matter consumption, it makes no difference if the power satellite self powers part of the way out or not. | ||
| + | |||
| + | |||
| + | <!-- == stuff to move == | ||
| + | >> We get the wages back at the company store where we charge them $200/kg | ||
| + | >> for steak. Just kidding! | ||
| + | > | ||
| + | > Not really kidding, though. The burdened cost of labor in orbit is indeed | ||
| + | > exorbitant, however you do the accounts. You should see the rent on a 30 m^2 | ||
| + | > studio per month! Orbital habitat is indeed the epitome of the company town. | ||
| + | > The 19th c. mining barons would salivate over the opportunities to exploit | ||
| + | > labor in this environment. I doubt modern financiers are all that much | ||
| + | > different. | ||
| + | |||
| + | I don't know how to solve this problem. I would think the | ||
| + | organization that was running the power satellite construction project | ||
| + | would want to keep their workers happy. However, don't assume the | ||
| + | workers are western. | ||
| + | |||
| + | >> My solution to this problem is to send workers up one way. I.e., they | ||
| + | >> would be expected to stay at least ten years. | ||
| + | > | ||
| + | > This isn't medically viable unless you have an artificial gravity | ||
| + | > environment. | ||
| + | |||
| + | Agree. And radiation shielding to Earth surface exposure as well, at | ||
| + | least for the inside. The problem comes from the interaction of | ||
| + | orbital mechanics, the slow trip up (needed to keep the reaction mass | ||
| + | cost down) and the lack of shielding during the trip back down to LEO. | ||
| + | The radiation exposure for the trip back may be reduced by draining | ||
| + | the Van Allen belt, but there does not seem to be a low cost way of | ||
| + | moving people to the construction site outside the cargo stacks. | ||
| + | |||
| + | > The marginal cost tradeoff is between transportation expense | ||
| + | > and habitat capital and operating expense. | ||
| + | |||
| + | That's sort of true. But when it takes 25 days to get up and 5 to get | ||
| + | back, the working come would be cut by 1/3 if you had the workers on a | ||
| + | 2 month schedule. Plus coming back they would probably accumulate a | ||
| + | lifetime radiation limit, if it didn't kill them. | ||
| + | |||
| + | > In terms of cost estimating, the easy was to deal with all this is to assume | ||
| + | > a fractional cost burden on powersat maintenance and then design habitat to | ||
| + | > that cost. It's not going to be possible to know a whole lot more at the | ||
| + | > current stage of maturity. | ||
| + | |||
| + | I don't understand maintenance. This is only about construction. I | ||
| + | have not yet considered where we base the human maintenance workers. | ||
| + | Any thoughts? In any case, shielding is a big problem no matter where | ||
| + | you base people in space. | ||
| + | |||
| + | Keith | ||
| + | --> | ||
| + | |||
| + | ==External Links== | ||
| + | *[https://en.wikipedia.org/wiki/Space-based_solar_power Wikipedia's take on the topic] | ||
[[Category:Earth Orbit]] | [[Category:Earth Orbit]] | ||
Latest revision as of 12:51, 9 April 2019
Space Based Solar Power is the concept of moving the collection of energy from Sol to Earth orbit in order to increase collection efficiency, eliminate weather, time-of-day, and seasonal outages, and reduce needed land usage. Energy collectable from orbit is a major factor in the first level of the Kardashev Scale.
Contents
What are Power Satellites?
They are a way to collect solar power out in space, usually GEO where the sun shines 99% of the time. Solar power on the ground has the problems of intermittency from clouds, night and the sun being low in the sky. Typically, ground solar in good locations averages about 20% of its peak rating. Power satellites are subject to short eclipses (up to 70 minutes) near the equinoxes around midnight. Because demand is low, the interruptions can be tolerated. With deep market penetration, the microwave beams can be crossed if the demand exceeds the capacity of the surface grid to redistribute power east to west or west to east.
They potentially scale to more than ten times the current energy needs of the human race. Started soon and pushed hard, they could end the build up of CO2 in the atmosphere and even reverse it.
If power satellites reach a high market penetration at times the power demand will go below their output. Power in excess of current demand can be fed to synthetic fuel plants solving the liquid transport fuel problem as well.
Methodology of This Work
The specifics in this study are less important than the analysis methodology. Important concepts include levelized cost of power, specific mass in terms of kg/kW, lift cost, ERoEI, and payback times. The attempt here will be to analyze specific examples but the details of choices such as PV vs thermal are less important than the analysis procedure.
Power Satellites and Energy Economics
In the absence of other forces (such as legal requirements to buy renewable energy) power satellites compete in the energy market. Of all energy forms, electrical energy is the ultimate standard commodity. When a customer plugs in a toaster, there is no way to tell what source the energy came from. At the end of the month, they pay the bill at the rate set by the power company under the oversight of a utility commission. One level up, the power companies are hemmed in by regulations that they buy (or make) the lowest cost electricity, with exceptions in some places that they have to purchase certain amounts of renewable energy. Wind and (ground) solar are both intermittent, requiring other sources or expensive storage to provide reliable power. The capital cost of intermittently run backup power either bankrupts the utilities or results in very high electrical rates. This is the current situation: the higher the fraction of renewable, the higher the consumer cost of electricity.
The reason for the higher cost for systems that includes a lot of renewable power is not hard to understand. Wind and solar are intermittent. If steady, reliable power is desired then alternate sources of power are required. The capital cost of these backup sources must be included in the systemwide average cost of power in addition to the capital and maintenance cost of the wind or solar.
Space based solar power is renewable but not intermittent. That should make it easier to sell power from space at a premium. However, governmental energy policy changes unpredictably over time. An alternative would be a "design to cost" effort where the target cost of power is low enough to get a large market share without government intervention. Competing on cost is the way discount suppliers of many commodities obtained a substantial market share. (Examples, Southwest Airlines, GEICO, Charles Schwab.)
Levelized Cost of Power
The formula for the levelized cost to generate electricity is here: [1]
This spreadsheet [2] assumes $1,600,000 per MW ($1600/kW) as the initial cost and 10% per year of the parts cost for maintenance. Power satellites supply base load. In the spreadsheet, it is assumed to be ~91% of the time. It may be higher.
The discount rate used in the spreadsheet is 6.8%, same as the US government uses for other sources. The accounting period is 20 years, and no salvage value is assumed.
The ratio between the $1600/kW cost and the cost that comes out of the formula (~2 cents per kWh) is approximately 80,000 to one. Electric power cost is proportional to the cost of a power satellite (or any power source that has no fuel cost and low maintenance) in this ratio for this discount rate and years of service.
The UK government has determined that 3.5% discount is proper for projects of this kind. Using 3.5%, the electric cost comes out at just over 1.5 cents per kWh and ~100,000 to one. Extending the accounting period to 30 years at 3.5% brings the cost of power down to 1.24 cents per kWh and a cost of power to cost of investment ratio to ~130,000 to one. It is a live spreadsheet; try your own numbers. A ratio of 80,000 to one is conservative.
To take market share from coal will require the cost to be less than 4 cents per kWh for electricity from coal. Three cents per kWh allows a capital cost of $2400/kW. That, or less, is the "design to cost" target.
Cost Allocations
The current model has the $2400 target cost (from levelized cost above) split out as follows:
- $200/kW for the rectanna ($1 B for 5 GW),
- $900/kW for the cost of parts and minor labor in space and
- $1300/kW (6.5 kg/kW[[3]] and $200/kg) for the cost of transport to GEO. (add pointer to sustech 2014 paper)
These numbers are targets which future work will firm up. If they go too high, something (like the cost charged for the electric power) will have to be adjusted. Of course, if they go too high, the entire idea needs to be reconsidered.
ERoEI (Energy Returned on Energy Invested) and Energy Payback Time
One of the metrics used to evaluate energy projects is energy return on energy invested. This is expressed as a ratio, and for shallow oil wells decades ago was typically 100 to one or higher. i.e., number of barrels of oil needed to drill an oil well divided into the number of barrels it produced. An alternate way more applicable to renewable sources is the energy payback time. It's typically about two years for PV or wind.
High ERoEI and short payback times usually accompany low cost.
Most of the energy embedded in a power satellite comes from the transport fuel.
Transport Energy
Combustion of hydrogen is 143 MJ/kg or 39.4 kWh/kg plus the energy needed to liquefy the hydrogen. Google for "A Future Energy Chain Based on Liquefied Hydrogen" (you may need to add Berstad) and go down to page 20. There they cite a number of ~6.5 kWh/kg to liquefy hydorgen. A large industrial plant might do a little better by warming the LNG before steam reforming with hydrogen to start the cooling. Ignoring that possible small improvement, the energy cost of LH2 is about 46 kWh/kg. It's hard to say exactly where you should measure the input energy, but the process to make hydrogen from natural gas is efficient, and (if we ship it as LNG) it only uses about 1.7% of the energy in a kg of natural gas to liquefy it. I.e., measuring at the well head will not make a great deal of difference. The CO2 released by steam reforming of natural gas is about 2.5 times the hydrogen produced.
The current LEO to GEO hydrogen consumption (using electric propulsion) is 4000 tons to get 15,000 tons to high orbit. On average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 tons of hydrogen reaction mass. I.e., 73% of the payload in LEO gets to GEO. At launch the average Skylon has 59 plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload 62 tons/11.84 tons or 5.25 kg/kg of payload.
The solar energy used to power the LEO to GEO transport is not included since it is outside the Earth system. (The capital cost of the propulsion power satellite is included in the financial models.)
For a power satellite specific mass of 6.5 kg/kW, a kW of power satellite (i.e., 6.5 kg) would use a little over 34 kg of LH2 to put it in GEO. Using 46 kWh/kg for the energy content of LH2, that's around 1566 kWh of energy per kW of power satellite.
Parts Energy
Without a detailed list of the parts, materials and mass in a power satellite, it's not easy to say how much energy goes into making the parts. Aluminum has the most embedded energy at 15 kWh/kg. But not very much will be aluminum. If we estimate 10 kWh/kg, the energy in the parts would be ~650 kWh, for a total of 2216 kWh per kW of capacity.
When the power satellite is turned on, it takes 92 days (at 100% on time) to repay the energy used to build it and move it to GEO.
That's a three-month energy repayment time. There are no other renewable proposals that are even close.
If the power satellites last 30 years, you get an ERoEI of 120 to one, as good as early shallow oil wells.
This is subject to adjustment as we settle on more accurate numbers in the design phase, but it is good enough to justify investigation in detail.
In his book on power satellites, John Mankins gives a payback time of 8 weeks. John uses the energy from physics, about 12 kWh/kg from the surface to GEO) (IIRC, it's actually 14.75 kW/kg)and doubles it twice for his estimate.
Power Satellite Types
Photovoltaic (PV) and Concentrated PV
Most designs for power satellites since the 1970s have been PV. PV has advantages, long experience powering communication satellites being important. However, PV suffers from relatively low efficiency (20%) and degradation from radiation. There are proposals by Robert Forward and Robert Holt on draining the van Allen belt [4]; however, just the presence of a substantial number of power satellites in GEO is expected to greatly mitigate the radiation from particles trapped in the Earth's magnetic field. (The particles are stopped by running into a power satellite. There are only about 3 kg of protons trapped in the belts.)
There are PV cells that range up to 40% efficient, but they require concentrated light and cooling. The work on thermal power satellites makes CPV possibly attractive, though there are problems with the limited supply of gallium which is used to fabricated the multi-junction cells.
Thermal
Thermal (heat engines) power satellites are expected to eventually range up to 60% efficient, similar to combined cycle plants on earth. This means they need about 1/3 of the light interception area of ordinary PV, which reduces station keeping from light pressure. However, they also need radiator area that is about twice the sunlight interception area, (Bejan, 1997, pg 495, ref Bejan, A. Advanced Engineering Thermodynamics, 2nd ed. New York: Wiley, 1997.) Counting both sides of the radiator makes the exposed area for thermal and photovoltaic power satellites about the same.
Common Considerations
Light Pressure and Mass
Light pressure is about 9 N/km^2
The original studies done in the late 1970s came up with a mass of ~10 kg/kW. More recent realistic studies have averaged around 7 kg/kW. A few studies have proposed designs under one tenth of a kg/kW. Very light designs require a lot of station keeping against light pressure where designs in excess of 5 kg/kW can average the light pressure over a year. Because a substantial fraction of the construction cost is for transport to GEO, the mass of a power satellite is as important a number as the lift cost to GEO. This analysis will use 6.5 kg/kW. The number can be adjusted in the spreadsheets.
Energy Transmission Loss
How efficient is the transmission of the energy with the microwave beam?
For economic analysis, 50%. The loss chain might be a little better with technical improvements, but not much. It means you generate two kW in space for one kW on the rectenna bus. That's been assumed in all the analysis here.
Transport Methods Surface to LEO
Falcon Heavy
Consider the projected Falcon Heavy, 53,000 kg to LEO, 121,400kg of RP-1. That's about 2.3 kg of fuel for every kg lifted to LEO (here I assume that the entire mass in LEO is either reaction mass for the trip up or can be converted to power satellite parts--this may not be reasonable). RP-1 is 42 MJ/kg, so the energy expended to LEO is about 96.2 MJ/kg or 26.7 kWh/kg. You also have to lift the reaction mass for the LEO to GEO leg so the fuel cost needs to be increased by around 20% giving 33.4 kWh/kg. If the reaction mass is hydrogen, it's energy content is not zero, hydrogen is close to 50 kWh/kg to make it and another 20 kWh/kg to make it into a liquid. So to move a kg from LEO to GEO would take 1/4 kg of LH2 at 70 kWh/kg or 17.5 kW/kg, for a total of ~51 kWh/kg. At 10 kg/kWe (on the ground) 510 kWh will be required to move a kW of power sat to GEO. At 100% on time, that's about 23 days to repay the energy. Unless I made an error, John's number is close enough. If only half of a Falcon Heavy payload becomes power satellite parts, John's estimate is very close.
Skylon
Much of the analysis been done using 50 kWh/kg as a ballpark number for hydrogen. It's good enough for rough calculations and it what it takes to make hydrogen if you are making it with electric power.
Combustion of hydrogen is 286 kJ/mol. Mole is 2.016 gm, so 496 moles in a kg, 143 MJ/kg or 39.4 kWh/kg. That's quite a bit less. The rough analysis have also been using 20 kWh/kg to liquify the hydrogen. That's way off. If you Google for "A Future Energy Chain Based on Liquefied Hydrogen" Berstad and go down to page 20, they cite a number of ~6.5 kWh/kg. We might do a little better because we can use warming the LNG to cool the hydrogen. That makes the energy content of the LH2 about 46 kWh/kg. It's hard to say exactly where you should measure the input energy, but the process to make hydrogen from natural gas is efficient, and it only uses about 1.7% of the energy in a kg of NG to liquify it. I.e., measuring at the well head will not make a great deal of difference. Still, this Wiki article needs to go into the thermodynamics of steam reforming.
Transport Methods LEO to GEO
The current LEO to GEO hydrogen consumption (using electric propulsion) is 4000 tons to get 15,000 tons to high orbit. On average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 tons of hydrogen reaction mass. At launch the average Skylon has 59 plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload 62/11.84 or 5.25 kg/kg of payload.
(Why hydrogen and not an inert gas? For a given amount of energy you can get considerably more exhaust velocity out of hydrogen.)
The solar energy used to power the LEO to GEO transport is not included since it is outside the system. (The capital cost of the propulsion power satellite is included in the financial models.)
Using my supported but perhaps optimistic number of 6.5 kg/kW, an installed kW would use a little over 34 kg of LH2 to get it in place. Using 46 kWh/kg for the LH2, that's around 1566 kWh per installed kW.
Without a detailed list of the parts materials and mass in a power satellite, it's not easy to say how much energy goes into the parts. Aluminum has the most embedded energy at 15 kWh/kg. But not very much will be aluminum. If we estimate 10 kWh/kg, the energy in the parts would be ~650 kWh, for a total of 2216 kWh per kW of capacity.
When the power satellite is turned on, it takes 92 days (at 100% on time) to repay the energy used to build it and move it to GEO.
That's a three month energy repayment time. I don't know of any other proposal that is even close. And the energy from a power satellite not intermittent.
If the power satellites last 30 years, you get an ERoEI of 120 to one.
This is subject to adjustment as we settle on more accurate numbers in the design phase, but it should be reasonably close.
ERoEI is an interesting metric, but the more important figure is the cost. Target cost is 3 cents a kWh falling to 2 cents within a few years. This just barely meets Gail's requirements. For a first approximation, the embedded energy in the parts and the energy required to make LOX are so small in comparison to RP1 or LH2 that they can be ignored.
It's surprising that even with a lower kg/kW number the energy payback time is longer for the Skylon.
Energy Payback Time, EROEI and Maximum Growth Rate
I recently ran an energy payback time for power satellites constructed using Falcon Heavy. It came in at around 8 weeks.
The current computation of LEO to GEO hydrogen consumption (using electric propulsion) is 4000 tons to get 15,000 tons to high orbit. On average, that makes a 15 ton Skylon payload 11.84 tons cargo and 3.16 tons of hydrogen reaction mass. At launch the average Skylon has 59 plus 3 or 62 tons of LH2. That makes the hydrogen per ton of payload 62/11.84 or 5.25 kg of hydrogen per kg of payload.
The solar energy used to power the LEO to GEO transport is not included since it is outside the system. (The capital cost of the propulsion power satellite is included in the financial models.)
Combustion of hydrogen is 286 kJ/mol. Mole is 2.016 gm, so 496 moles in a kg, 143 MJ/kg or 39.4 kWh/kg. If you Google for “A Future Energy Chain Based on Liquefied Hydrogen” Berstad and go down to page 20, they cite a number of ~6.5 kWh/kg. We might do a little better because we can use warming the LNG to partly cool the hydrogen. That makes the energy content of the LH2 about 46 kWh/kg. It’s hard to say exactly where you should measure the input energy, but the process to make hydrogen from natural gas is efficient, and it only uses about 1.7% of the energy in a kg of NG to liquify it. I.e., measuring at the well head will not make a great deal of difference. Still, we need to dig into the thermodynamics of steam reforming.
Using s perhaps optimistic number of 6.5 kg/kW, an installed kW would use a little over 34 kg of LH2 to get it in place. Using 46 kWh/kg for the LH2, that’s around 1566 kWh per installed kW.
Without a detailed list of the parts materials and mass in a power satellite, it’s not easy to say how exactly much energy goes into the parts. Aluminum has the most embedded energy at 15 kWh/kg. But not very much will be aluminum. If we estimate 10 kWh/kg, the energy in the parts would be ~650 kWh, for a total of 2216 kWh per kW of capacity.
When the power satellite is turned on, it takes 92 days (at 100% on time) to repay the energy used to build it and move it to GEO.
That’s a three month energy repayment time. We know of no other energy proposal that is even close. And the energy from a power satellite not intermittent.
If the power satellites last 30 years, you get an ERoEI of 120 to one.
This is subject to adjustment as we settle on more accurate numbers in the design phase, but it should be reasonably close.
ERoEI is an interesting metric, but the more important figure is the cost. Target cost is 3 cents a kWh falling to 2 cents within a few years. This just barely meets Gail’s requirements.
By the criteria given here https://en.wikipedia.org/wiki/Energy_cannibalism and here https://web.archive.org/web/20090817071517/http://www.climate2008.net/?a1=pap&cat=1&e=61 a power satellite growth rate of lower than 360% per year would result in lowering GHG emissions.
Reliability
Electric power needs to be reliable. First, the power satellite size is only 5 GW. The target number is 3000 for 15 TW. There would be spares sending power to low priority loads that could be switched in less than a second to replace a higher priority failed one. Plus we would still have the grid to distribute electricity from the remaining powered rectennas, and for a long time, there would be other generation in the mix.
None the less, there are ways we could lose the whole fleet of them in an instant if they were not designed to deal with it. In the year 774 or 775 the Earth seems to have been hit with either a unprecedented solar flare or a fairly close gamma ray burst. The latter are typically a few seconds, the former might take a few hours. In any case, it put a serious kink in the carbon 14 for the next growing season. Such an event would take out the controls for any power satellite that did not have enough shielding around the control computers. The shielding needed against these 1000 year events is considerably more than the worst solar flares observed to date.
Unlikely as they are, GRB or intense high energy solar flares are a concern that requires mitigation and recovery strategies such as watch dog timers and hardened reboot memory. Radiation resistance is an argument in favor of rotating machines rather than PV.
A solar flare can be seen coming and outside workers would probably have time to reach shelter. A GRB would be over before the workers had a chance to move. Neither are serious problems for people behind shielding good enough to stop cosmic rays.
Transport Earth to LEO
SpaceX
SpaceX may not get the transport cost down low enough. It has to be to be SSTO or possibly TSTO runway operations.
SpaceX _will_ eventually get the cost to GEO down by a full order of magnitude, a remarkable achievement. Unfortunately this won't do it for power from space, it takes _two_ orders of magnitude reduction. Elon Musk knows this. It might be why he is so down on power satellites.
Note Oct 15,2016.
Musk was recently talking about a rocket with a cost of putting cargo into a Mars trajectory for $143/kg. That's remarkable and is low enough for power satellites to make economic sense.
Skylon
Until Reaction Engines demonstrated their high performance precooler, there were no realistic SSTO proposals out there.
www.reactionengines.co.uk/space_skylon.html
Skylon Doesn't Cause Much Ozone Damage (NOx)
NOAA worked out that up to a million Skylon flights per year there is little damage to the ozone. There is no point in solving the carbon and energy problem with power satellites if the cost is a billion cases of skin cancer.
The NOAA people put a lot of effort into modeling the problem, hundreds of hours of supercomputer time on the models, writing a paper and getting it through peer review. Highly appreciated.
The paper is available online at
http://onlinelibrary.wiley.com/doi/10.1002/2016EF000399/full
Click on the PDF symbol next to the journal title.
LEO to GEO
Space Junk
Back in the late 70s, Boeing proposed building power satellite in LEO and then self powering to GEO (using ion engines or arcjets). They even did some nice artwork. But even in those days there was enough space to make this a very risky move and it was abandoned. HKH redid the math in recent years using the density of space junk given in the Wikipedia article. The result was that a power satellite would be hit almost 40 times while self powering to GEO. Almost all the hits are below 2000 km altitude.
Building power satellites in LEO would work, it's just they could not be moved to where they are useful unless the plan includes cleaning up the space junk first.
Engines
Arcjet
VSMIR
Power
Tug Rectenna
Increasing the frequency to 25 GHz and reducing the distance to half allows reducing the tug rectenna to 500 m.
This has not been optimized, nor have the tracking details worked out.
Worker Transport
Getting workers out to 12,000 km takes either a fast transport to keep the radiation exposure from the inner van Allen belt down or sending them up inside cargo containers. If they go up with power satellite parts around them for shielding, the trip is about 25 days. The return trip is shorter, around 5 days, but unless a lot of shielding is taken
Propulsion Power Satellite
Reaction Mass
Construction Orbit
Construction Site
Tentatively we have selected 10,400 km, less than one third of the way to GEO. This is in a six hour orbit orbit. The choice is based on this altitude being the low radiation zone between the inner and outer van Allen belts. The orbit is subject to tradeoff/optimization studies which have not been done yet.
Platform (JIG)
Even more tentative, we have envisioned a kind of "dry dock" for power satellites. Big frame of beams to move cargo from the stacks to the work sites where the power satellites are constructed. We also project a rotating habitat with the spin axis pointing solar north/south and a concentrating reflector to bring light inside through a window.
Habitat--Company Town?
On the roughest of analogies dating back to Liberty ship construction in WW II, it might take 400 construction workers for the 10 per year pilot construction plant. This includes families. The shielding on the habitat will need to be ~six tons per square meter to reduce the cosmic radiation to the level seen on Earth.
The consequence for a 50 m habitat is 60,000 tons of shielding, about $9 B in lift cost at $150/kg.
It has to be a spinning habitat. One thing learned from the ISS is that neat as zero g is, human do not do well health wise in long term zero g. The spin rate for one g at the equator is 6 RPM. Do we spin the shielding or just the habitat? In either case, there is a considerable amount of rotational kinetic energy in the habitat. Whatever is used for a bearing must be proof against lockup.
There is a reason for families. We can't expect construction workers to live like monks or nuns. Taking them to and from 10,400 km (6 hour orbit) is either slow or very expensive in reaction mass and power. It is relatively easy to ship the workers and families up. They are shielded by containers of parts for the 25 days it takes to transit up. But there are no parts coming back down so shielding for returning workers would have to be carried at great cost. Alternately, they could go up in the habitat if it was constructed in LEO.
About the interaction of radiation, workers and transport . . . we might be able to build power satellites entirely using robots directed from the ground or by AIs. We don't have such robots/AIs yet, but if the development time is short and the cost less than $9 B, that may be the way to go. (Teleoperated robots are closer and a 6 hour orbit does not induce as much speed of light delay as GEO.) I would be OK with that, though saddened by the loss of human experience. Assuming we don't have robots building power satellites, or at least they need help from people, then we have to have people in space. For social and economy of scale reasons fewer than about 200 may not make sense. If the ISS is any indicator, one quarter of them will be working on maintenance to keep the habitat liveable.
A power satellite project makes a lot of money but can it afford 200 workers in space? Perhaps the least complicated analysis is to take the income stream from 10-12 power satellites per year. That seems to be the minimum were transport economies of scale kick in. 11 power satellites at $11 billion each is $121 B. A thousand people would be building $121 M per person, 500 would be building $242 M each. A pay rate of a million per person per year would make the labor charges on the product under half a percent.
We get the wages back at the company store where we charge them $200/kg for steak. Just kidding!
After feeding the workers, the "used" food becomes part of a power satellite so the effective cost to feed them is zero. If there is nothing else to use it for, each power satellite needs a substantial "space anchor." A "space anchor" is just a multi ton mass (anything will do) on the end of a long string. It is connected to the transmitter disk edges by a bridal and winches. It eliminates using reaction mass for pointing the power satellite. (Gravity gradient stabilization.)
So we can pay the workers and feed them. Next problem is getting them out to the construction site. If we use 10,400 km (in the radiation minimum between the van Allen belts) then the time for the reference beamed energy transportation system is about 25 days up and about 5 days back. In the Apollo program, http://www.braeunig.us/apollo/VABraddose.htm, the astronauts skirted around the belts and went fast so they didn't spend time in them. For power satellites we have to bull right through the hottest part of the Van Allen belt and slowly too due to the orbital mechanics of spiral orbits.
However, we have something on the trip up the Apollo astronauts didn't have, tens of thousands of tons of power satellite parts which can be used for shielding. The scale of the cargo stacks is more or less set by beamed energy microwave optics used to power the stack out to the construction site. If made of Skylon sized containers, a cargo stack has 11 layers of 91 containers per layer. If the modules for human transport are buried a few layers down and in the center of the stack, it's hard to imagine the relatively low radiation of the worst part of the belt giving them much exposure (though it should be calculated).
An alternative would be to build the habitat in LEO and send it up with the workers inside. Depending on the propulsion power available, this could take a couple of months.
The exposure on the way down is 1/5th the time, but with no cargo to shield them, the radiation exposure would be much larger, perhaps lethal.
My solution to this problem is to send workers up one way. I.e., they would be expected to stay at least ten years. That means that (unless you plan on using monks) we have to send up families. That means children, and that means controlling the radiation in the construction habitat to no worse than the level at Denver and spinning the habitat to one g.
Limited Recycling
Most food for the workers can be shipped up. It is essentially free since after people eat it, it can all be recycled into parts of a power satellite. Not so with fresh food that cannot survive a month shipping. Salad greens need to be grown in the habitat. This does not look like a hard problem and may eliminate some of the atmosphere contaminate problems that require burners in submarines.
Self Power (Out to GEO)
In terms of reaction matter consumption, it makes no difference if the power satellite self powers part of the way out or not.